
Quelle: Wikimedia
Dieses Tutorial ist eine Einführung für alle, die ein (wissenschaftliches / musiktheoretisches) Interesse an den verschiedenen Methoden haben, die zur Analyse von Musik verwendet werden. Am Ende des Tutorials findest du darüber hinaus Links für weiterführende Anleitungen zu den jeweiligen Themen.
Inhalt
Allgemeine Überlegungen
Musiktheoretische Symbole (zum Beispiel Funktionssymbole, Stufensymbole, Changes, etc.) und auch Satzmodelle (zum Beispiel die Quintfallsequenz, der Pachelbel-Bass bzw. Parallelismus, etc.) sind gedankliche Konstruktionen, um einen speziellen Ausschnitt aus der uns umgebenden Umwelt besser verstehen zu können. Solche Konstruktionen sind dabei nicht nur in einer Fachwissenschaft wie der Musiktheorie hilfreich, sondern auch im alltäglichen Leben:
Das, was wir unter ›Zeit‹ verstehen, ist zum Beispiel sehr abstrakt und nur schwer zu begreifen. Man kann das Gefühl haben, dass Zeit schnell oder unendlich langsam vergeht oder sogar still steht. Zeit kann ein Zeitpunkt sein oder wie ein Fluss veranschaulicht werden, der kontinuierlich in Richtung Zukunft ›fließt‹ und der keinen Anfang und kein Ende hat. ›Zeit‹ hat Menschen in der Philosophie, Soziologie und Naturwissenschaften beschäftigt, doch muss man nicht philosophieren, um mit Zeit praktisch umgehen zu können. Üblicherweise veranschaulichen wir uns Zeit über eine ›Zeitleiste‹ oder einen ›Zeitstrahl‹:
Indem wir auf einer Zeitleiste Ereignisse markieren, die wir uns als Zeitpunkt oder Zeitintervall vorstellen, ritzen wir Markierungen in das Kontinuum ›Zeit‹ wie in die Rinde eines lebenden Baumes. An den Stellen, an denen wir die Zeit auf diese Art ›verletzt‹ haben, stirbt ihre Bewegung und wir können über ein Ereignis in der Zeit wie über einen unbeweglichen Gegenstand nachdenken (zum Beispiel über J. S. Bach oder Britpop). Zeitmarkierungen sind also abstrakte, gedankliche Gliederungspunkte, damit wir mit dem eigentlich Unfassbaren im Alltag besser umgehen können. Im Laufe der Zeit hat sich ein allgemein gültiger Standard für die Gliederung von Zeit durchgesetzt, der uns hilft, vom Aufgang der Sonne bis zu ihrem Niedergang besser durch den Tag zu hetzen.
Sekunden, Minuten und Stunden sind uns also nicht durch die Umwelt vorgegeben, sondern eine Vorstellungen, die wir in der Regel mit einer bestimmten Absicht verwenden. Und ohne Berücksichtigung dieser Absicht lässt überhaupt nicht sinnvoll entscheiden, ob unsere Zeiteinteilung angemessen oder unangemessen ist. In Bezug auf eine Meditation zum Beispiel dürfte die Einteilung von Zeit in Minuten unangemessen sein, weil sie das Erreichen des In-Sich-Ruhens erschwert. Die Ruhe, die in der Meditation erzielt werden soll, ist kaum zu vereinbaren mit minutiösen Gedanken (»in wie vielen Minuten muss ich aufhören, um heute noch dies oder jenes schaffen zu können«). Im Hinblick auf das Fahren mit dem ICE hingegen ist genau diese Zeiteinteilung angemessen, denn wir müssen nicht planlos auf dem Bahnhof umherirren, bis wir zufällig einen Zug unserer Richtung finden. Darüber hinaus ist es nützlich, bei Verspätungen ganz genau auf die Uhr zu schauen (denn ab 30 Minuten gibt es Geld).
Wie Minuten das Kontinuum Zeit teilen, markieren die Töne einer Tastatur das Kontinuum der Tonhöhe. Und die auf modernen Flügeln übliche Einteilung (die sogenannte gleichstufig gleichschwebende Temperatur) wird in der Beschäftigung mit alter Musik als unangemessen, in Bezug auf spätromantische Klaviermusik als angemessen beurteilt.
Die Zeiteinteilung ist also eine gedankliche Konstruktion und die Töne unseres Tonsystems sind auch eine (Uhren und Tastaturen sind technische Hilfsmittel dafür). Speziellere Konstruktionen für die theoretisch-wissenschaftliche Beschäftigung mit Musik sind Satzmodelle wie die Quintfallsequenz, Funktionszeichen und Change-Symbole, Lautstärkediagramme, Buchstabenfolgen (AABA) usw. In der Analyse schnitzen wir nun in den komplexen und in seiner Gesamtheit ›unfassbaren‹ Gegenstand Musik unsere gedanklichen Markierungen (C-Dur, G-Dur, E7, a-Moll, Tonleiter im Bass, strukturelle Sekundschritte der Melodie) und können uns dadurch Teilaspekte (z.B. die Harmonik) einer Musik veranschaulichen. Dadurch werden diese Teilaspekte unserem Handeln verfügbar (zum Beispiel können wir musikbezogene Ansagen vor einem Orchester machen oder Choralsätze oder Rocksongs schreiben). Und wie es im Zusammenhang mit der Zeit schon festgestellt worden ist, sind Diskussionen über die Angemessenheit solcher gedanklichen Konstruktionen ohne die Berücksichtigung der Absicht unsinnig. Wenn jemand etwas über harmonische Verläufe einer bestimmten Musik erfahren möchte, werden ihm auf der einen Seite Rhythmusdiagramme wenig nützen. Auf der anderen Seite gibt es funktional äquivalente Methoden der Analyse (z.B. Funktionsdiagramme, Satzmodelle, Tonleiterverläufe im Sinne Schenkers etc.), wobei jeweils diejenige am positivsten zu bewerten ist, mit der sich die Interpretation eines musikalischen Sachverhalts am besten veranschaulichen lässt. Frei nach dem indonesischen Sprichwort...
Wer nur einen Hammer hat, für den sieht jedes Problem wie ein Nagel aus
...ist jede Methode der musikalischen Analyse lediglich ein Werkzeug. Dabei bestimmt die Anzahl unserer Werkzeuge den Grad unserer Freiheit im Umgang mit den Gegenständen (Nägeln, Tönen, Harmonien und anderen Bildern an den Wänden unseres Verstandes).
Stufentheorie

Geschichte
Stufenzeichen finden sich bereits im 18. Jahrhunderts bei Johann Philipp Kirnberger (1721−1783) und Georg Joseph Vogler (1749−1814). Weiterentwickelt und systematisch verwendet wurden die Stufenzeichen dann von Gottfried Weber (1779−1839), der als Begründer der Stufentheorie gilt. Weber schlug im zweiten Band seines Versuch[s] einer geordneten Theorie der Tonsetzkunst zum Selbstunterricht vor:
Unsere Bezeichnung des Sitzes der Harmonien. § 151.
Noch allgemeiner, als im § 149 durch teutsche Buchstaben geschehen, nämlich nicht auf eine bestimmte Tonart beschränkt, sondern auf eine jede passend, kann man die Gesamtheit ihrer Harmonieen [!] vorstellen, wenn man, statt der teutschen Buchstaben, die römische Zahl der Leiterstufe setzt, und zwar, statt der grosse, oder kleinen Buchstaben, grosse, oder kleine römische Ziffern, und diese, gerade wie sonst die teutschen Buchstaben, mitbezeichnet.
- Als Ziffer rechts neben dem Stufensymbol war anfangs nur die 7 gebräuchlich. Anstelle der durchgestrichenen 7 kann dann das in der Popularmusik für große Septimen gebräuchliche Symbol 7+ verwendet werden.
- Ernst Friedrich Richter verwendete zusätzlich zu den Stufenzeichen Generalbassziffern für Akkordumkehrungen, die dann rechts neben den Stufenziffern notiert werden. In diesem Fall ist es auch möglich, die 7 wie im Generalbass als diatonische Septime zu verwenden und nur Abweichungen mit Vorzeichen zu kennzeichnen.
- Chromatische Veränderungen der Tonstufe können durch ein ♯ oder ♭ vor der Ziffer angezeigt werden.
Stufensymbole und Jazz-/Rock- und Popmusik
Das Verwenden von Stufenzeichen zur Chiffrierung harmonischer Verläufe ist in Analysen zur Popularmusik weit verbreitet. In seinem Aufsatz »Form in Rock Music. A Primer« (2005) verwendet John Covach z.B. im Rahmen von Formanalysen eine sehr ökonomische Art der Chiffrierung harmonischer Verläufe, indem er arabische Zahlen (für die Anzahl von Takten) mit Kleinbuchstaben kombiniert, die für bestimmte Harmoniepatterns stehen.

John Covach, »Form in Rock Music. A Primer«,
in: Engaging Music. Essays in Music Analysis, New York 2005, S. 65–76. Quelle der Sounddatei: YouTube.
Probleme
Problematisch ist, dass es gerade im Bereich der Popularmusik nicht selten vorkommt, dass sich bei einem Harmoniepattern eine I oder i nicht ohne Willkür festlegen lässt. Zum Beispiel ist es sowohl angemessen, das gängige Pattern Am - F - C - G zu chriffrieren als
- i - VI - III - VII oder
- vi - IV - I - V,
da die Hörweise wechseln kann, je nachdem, welche Stimmführung erklingt und ob das Pattern einmal oder mehrmals hintereinander zu hören ist.
Auch andere Probleme wie z.B. die Chiffrierung vom Quartsextvorhalt der Dominante und Zwischendominanten haben dazu geführt, dass Stufensymbole mit einigen Zeichen der Funktionstheorie vermischt verwendet werden.
- Anwendungsbeispiel zur Stufentheorie anhand des Themas der Klaviersonate Es-Dur KV 281 von W. A. Mozart
Funktionstheorie

Geschichte
Begründer der Funktionstheorie war Hugo Riemann (1849−1919). Die Symbole, die er sich zur Chiffrierung ausgedacht hatte, sahen allerdings zu seiner Zeit noch ganz anders aus als die heute gebräuchlichen Funktionssymbole. Das lag insbesondere daran, dass Riemann ein Dualist war, das heißt: Riemann ging davon aus, dass die harmonische Logik in Dur durch die Obertonreihe, in Moll durch eine Untertonreihe bestimmt sei. Die Basis des C-Dur-Dreiklangs ist demnach C (der C-Dur-Dreiklang kommt in der Obertonreihe als 4., 5. und 6. Oberton vor), die Basis des c-Moll-Dreiklangs jedoch g (gedacht über eine spiegelbildlich zur Obertonreihe konstruierte Untertonreihe):
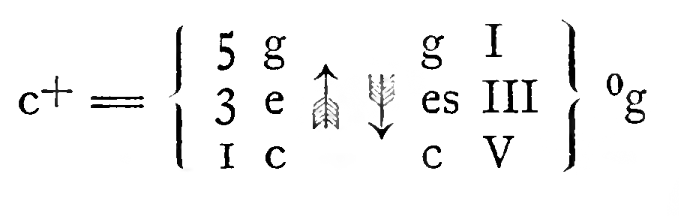
Die folgende Abbildung zeigt eine Buchstabenchiffrierung, wie sie Riemann 1898 am Ende seiner Geschichte der Musiktheorie abgebildet und zu Chiffrierungen anderer Musiktheoretiker in Beziehung gesetzt hat:

Riemanns Absicht war es, mit den Funktionszeichen die harmonische Analyse zu vereinfachen. Einerseits wollte er dasselbe Zeichen für die verschiedenen Akkordumkehrungen verwenden können. An der Chiffrierung der Umkehrungen eines Dominantseptakkords im Generalbass störten ihn die verschiedenen Bezifferungen für ein und dieselbe Funktion (im Beispiel ein dominantisches G-Dur, dass sich nach C-Dur auflöst):
Andererseits wollte Riemann durch Verallgemeinerung die »Loslösung der Bezeichnung von der einzelnen Tonart« erreichen. Doch wie schon bei der Buchstabenchiffrierung (oben) spiegeln auch Riemanns Funktionszeichen sein dualistisches Denken. Riemann verwendete dafür das heute nicht mehr gebräuchliche o-Zeichen vor Funktionssymbolen für Moll-Akkorde:

Viele Autoren wie Max Reger und Hermann Grabner haben sich im Anschluss an Riemanns Publikationen um eine weitere Vereinfachung der Funktionstheorie bemüht. In Deutschland durchgesetzt hat sie sich über die dritte Auflage der Harmonielehre von Wilhelm Maler (Beitrag zur durmolltonalen Harmonielehre, unter Mitarbeit von Günter Bialas und Johannes Driessler, 1950). Maler hat die Funktionstheorie weitgehend vom Dualismus bereinigt. Der folgenden Abbildung lässt sich auch entnehmen, warum der Funktionstheorie Riemanns während der Nazizeit und teilweise auch in den ersten beiden Jahrzehnten nach dem Krieg gegenüber den Schriften von Ernst Kurth, Heinrich Schenker und Arnold Schönberg in Deutschland eine ungebrochene Tradition haben konnte:
Seit den 1970er Jahren wurde die Funktionstheorie dann von Diether de la Motte (1928−2010), der bei Wilhelm Mahler in Detmold Komposition studiert hatte, in seinen wirkungsmächtigen Taschenbüchern weiterentwickelt. Und ein Schüler von Diether de la Motte war Clemens Kühn (* 1945), der in seinen prominenten Publikationen ebenfalls die Funktionstheorie favorisiert hat. Die folgende Tabelle gibt einen Überblick über heute gebräuchliche Symbole der Funktionstheorie.
- Anwendungsbeispiel zur Funktionstheorie anhand des Themas der Klaviersonate Es-Dur KV 281 von W. A. Mozart
Auch in der Analyse von Popmusik ist in Deutschland gelegentlich die Funktionstheorie verwendet worden. Das folgende Beispiel zeigt eine harmonische Analyse der Basslinie des Songs A Whiter Shade Of Pale (1967) der Band Procol Harum von Manfred Schuler (1931−2001):
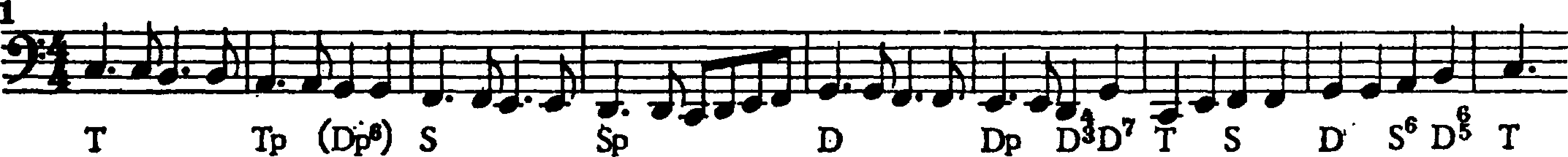
Manfred Schuler, »Rockmusik und Kunstmusik der Vergangenheit. Ein analytischer Versuch«, in: Archiv für Musikwissenschaft 35 (1978), S. 135‐150. Quelle der Sounddatei: YouTube
Und in dem Aufsatz »Musikalische Analyse und Sound« verwendet Heinz Bamberg die Funktionstheorie zur harmonischen Chiffrierung im Rahmen eines Songvergleichs:

Heinz Bamberg, »Musikalische Analyse und Sound«,
in: Beiträge zur Popularmusikforschung 07/08 (1989), S. 84‐92, URN: urn:nbn:de:hebis:26‐opus‐53300«.
Die Aufsätze von Schuler und Bamberg stammen aus den 1970er und 1980er Jahren, also aus einer Zeit, in der die Verwendung der Funktionstheorie auch in der deutschsprachigen Musikwissenschaft verbreitet war. In aktuellen Publikationen ist das Verwenden von Funktionssymbolen zur harmonischen Analyse dagegen nicht mehr üblich.
Probleme
Ein bekanntes Problem der Funktionstheorie ist z.B. die Chiffrierung des verminderten Akkords in Moll, der sich zwar als verkürzter Dominantseptakkord, nicht jedoch angemessen als ii. Stufe in Moll bezeichnen lässt. Das gleiche gilt für den halbverminderten Septakkord und die Chiffrierung von Sequenzen. Hierzu kannst du mehr in dem Tutorial Sequenzen und die Funktionstheorie erfahren.
Satzmodelle
Satzmodelle
Geschichte
Als Satzmodelle werden »Satztypen und -formeln des 15. und 16. Jahrhunderts« bezeichnet, auf die der Musikwissenschaftler Carl Dahlhaus 1968 in seiner Habilitationsschrift hingewiesen hat.
Die charakteristischen Schemata der tonalen Harmonik, die "vollständige Kadenz" [...], die "Quintschrittsequenz" [...] und der "Dur-Moll-Parallelismus" [...] sind in satztechnischen Formeln des 16. und des frühen 17. Jahrhunderts vorgebildet. Die äußere Übereinstimmung ist aber keine genügende Rechtfertigung einer tonalen Interpretation. Die Formeln sind zunächst nicht in einem Akkordsystem begründet, sondern umgekehrt: Das System ist aus einem Zusammenwachsen der Formeln hervorgegangen; das tonale Prinzip, das in der theoretischen Darstellung als Anfang erscheint, ist geschichtlich das zuletzt Erreichte.
Dahlhaus, Untersuchungen, S. 92.
Martin Eybl hat im Anhang seines Buchs Ideologie und Methode. Zum ideengeschichtlichen Kontext von Schenkers Musiktheorie (= Wiener Veröffentlichungen zur Musikwissenschaft 32), Tutzing 1995 (Dissertationsschrift) eine umfassende und äußerst komprimierte Übersicht zu Satzmodellen publiziert. Auf S. 155 beispielsweise finden sich unter der Überschrift II.4 7–6-Ligaturenkette Beispiele zu Quintfallsequenzen, zum Parallelismus und zum synkopierten Fauxbourdonsatz. Die Beispiele II.7 bis II.11 zeigen verschiedene Satzmodelle wie z.B. den Oberstimmensatz der Quintanstiegssequenz und Vorhaltsbildungen, die sich als Formen der Quintfallsequenz interpretieren lassen.

Aus: Martin Eybl, Ideologie und Methode. Zum ideengeschichtlichen Kontext von Schenkers Musiktheorie (= Wiener Veröffentlichungen zur Musikwissenschaft 32), Tutzing 1995, S. 155–156 (Anhang).
Auch wenn die theoretische Reflexion von Satzmodellen erst in der zweiten Hälfte des 20. Jahrhundert eingesetzt hat, waren Satzmodelle schon im 18. und 19. Jahrhundert teil einer praktischen Musikausbildung. Die folgende Abbildung zeigt Gerüstsätze und Diminutionen eines Satzmodells in der Anleitung Die Grundsätze der musikalischen Komposition (1853) von Simon Sechter:

Eine erste didaktische Ausarbeitung des Themas Satzmodelle für das musikalische Hören findet sich in der 1998 erschienenen Gehörbildung von Ulrich Kaiser, in der die klassischen Satzmodelle als Modelle für das mehrstimmige Hören eingesetzt werden. Ein Vorzug von Satzmodellen dürfte darin liegen, dass sie geeignet sind, sowohl melodische als auch harmonische Aspekte tonaler Musik sinnlich erfahrbar zu machen.
Beispiele
Aus der Vogelperspektive lassen sich Sequenzen im Allgemeinen unterscheiden in
- Sequenzen, die stufenweise auf- oder abwärts führen und
- Sequenzen, die terzweise auf- oder abwärts führen.
Stufenweise voranschreitende Sequenzen lassen sich in der Regel als eine Form der Quintfallsequenz verstehen, z.B. als
- stufenweise abwärts führender Quintfall:
- oder als stufenweise aufwärts führender Quintfall:
Und Sequenzen, die terzweise voranschreiten, lassen sich in der Regel als Ausprägung eines Parallelismus (Pachelbel-Modell) verstehen:
Auch in der Analyse von Popularmusik lassen sich Satzmodelle gewinnbringend einsetzen. Der Verse von »I Want To Hold Your Hand« von The Beatles beispielsweise lässt sich über das Satzmodell Parallelismus verstehen:
Probleme
Zur Analyse mithilfe von Satzmodellen hat Ulrich Kaiser geschrieben:
Ihr Hauptproblem liegt darin, dass sie einen musikalischen Verlauf zerteilt, und zwar in Satzmodelle und Nicht-Satzmodelle. Einwände, die gegen Satzmodellanalysen immer wieder erhoben werden, erinnern zu Recht daran, dass ein Zerlegen von Musik keine musikalische Analyse sei, weil das synthetische Moment fehlen würde, also im Falle einer Satzmodell-Analyse das Bestimmen der Funktion von Satzmodellen für das Werkganze. Bezieht man den Begriff Satzmodell ausschließlich auf die Dimension, in der sich die Notenbeispiele in den Schriften von Carl Dahlhaus bewegen, ist dieser Vorwurf sicherlich naheliegend. Satzmodelle transportieren zwar mehr Informationen zur Stimmführung als Funktions- oder Stufensymbole, zur Veranschaulichung der Formfunktion von Satzmodellen für das Werkganze benötigt man jedoch weitere, übergeordnete Modelle.
Ulrich Kaiser, »Vom Satzmodell zum Modell«, in: ZGMTH 13/Sonderausgabe [Special Issue] (2016), S. 135–153.
Grafische Analyse
Die Grafische Analyse (Reduktionsanalyse)
Geschichte
In einer Grafischen Analyse oder Reduktionsanalyse wird versucht, in einer grafischen Darstellung das Notenbild einer Komposition auf einen Gerüstsatz zu reduzieren. In einem solchen Analysegrafen werden Rhythmik und motivisch/thematische Besonderheiten vernachlässigt. Heinrich Schenker hat Theorie und Methode der grafischen Analyse in Wien entwickelt, insbesondere durch seinen 1939 emigrierten Schüler Felix Salzer wurde sie in Nordamerika intensiv rezipiert und ist dort heute weit verbreitet. Martin Eybl hat darauf hingewiesen, dass sich Schenkers Konzept mit dem Aufbau des psychischen Apparats bei Sigmund Freud (Ich, Über-Ich, Es) in Beziehung setzen lässt. Da weder in der Musik noch der Psyche Tiefenstrukturen faktisch gegeben sind, lassen sich Schenkers und Freuds Ideen kulturhistorisch auch als Denkfiguren verborgener Ordnungen interpretieren, mit dem eine intellektuelle Elite Wiens um die Jahrhundertwende auf das Zerbrechen äußerer Systeme (politischer und kultureller) reagiert hat.
In grafischen Analysen kennzeichnen Notenlängen die strukturelle Bedeutung einer Tonhöhe und nicht die spezifische Länge eines Tons. Im Bereich der Popularmusikanalyse ist das hilfreich, weil Tonhöhen gewichtet werden können, ohne dass deren Rhythmus notiert werden müsste. Damit wird die Schwierigkeit umgangen, das Mikrotiming in Popularmusik mit traditioneller Musiknotation skizzieren zu müssen. Zur Chiffrierung der Harmonik werden in grafischen Analysen nach H. Schenker Stufensymbole (s.o.) verwendet.
Heinrich Schenker hat seine Methode an den sogenannten Meisterwerken der Musik entwickelt. Die verschiedenen Schichten werden als Vorder-, Mittel- und Hintergrund (Ursatz) bezeichnet. Den Begriff des Ursatzes als Hintergrund einer Musik verwendet Schenker allerdings erst seit 1926. Die folgende Abbildung zeigt mögliche, im verborgenen wirksame Hintergrund-Sätze für tonale Musik:

H. Schenker, Der freie Satz, Wien 1935,
Anfang (Figurentafeln), S. 2, Figuren 9−11.
Beispiele
Schon vor der Annahme eines Ursatzes sind Schenkers Analysen durch eine starke Reduktion des Notenbildes charakterisiert. Die folgende Analyse der Exposition des Kopfsatzes der Sonate Facile KV 545 von W. A. Mozart hat Schenker im 4. Heft der Zeitschrift Der Tonwille im Jahr 1923 publiziert:

H. Schenker, Der Tonwille, 1923, Heft 4, Beilage
Quelle: YouTube
Mehr zur Analyse dieser Exposition kannst du erfahren in: Schenker reloaded – Eine Einführung in die graphische Analyse.
Die folgende Abbildung zeigt eine grafische Analyse von Walter Everett zu dem Song »I Want To Holf Your Hand« von The Beatles. Everett interpretiert hier als Hintergrund des Songs eine Kadenz (erkennbar an den Stufensymbolen I – III – IV – V –I):

Walter Everett, The Beatles As Musicians. The Quarry Men through Rubber Soul, Oxford und Ney York 2001, S. 199.
Probleme
Während die praktische Seite der Analyse nach Heinrich Schenker geschätzt wird, weil sich mit ihr Spannungsbögen und musikalische Wirkungen veranschaulichen lassen, die mit anderen Methoden nur schwer oder gar nicht fassbar sind, ist die Kritik meist auf einer anderen Ebene angesiedelt. Susanne Westenfelder hat dazu geschrieben:
In Schenkers Analyseansätzen klingt ein Gedankengut an, das – obgleich Schenker selbst jüdisch war – den Nationalsozialismus ideologisch berührt: Ein missverstandener Darwinismus (missverstanden, da laut dem bekannten Postulat „Survival of the fittest“ sich eben nicht die „fittesten“ Tierchen durchsetzen, sondern die am besten angepassten) durchzieht seine Ausführungen. In seinen Texten finden sich unüberschaubar viele Zeugnisse einer chauvinistischen und rassistischen Haltung. [...]
Eine Analysemethode, in der nur die stärksten Töne bestehen und weniger starke eliminiert werden, in der eine Hierarchisierung der Klänge den Kern der analytischen Arbeit ausmacht, in der der ›natürliche Zeugungswille‹, die ›Triebkraft‹ der Töne das Stück formt und in der restaurativ das Ergebnis der Betrachtung – der ›Ursatz‹ – bereits vor der Analyse des Werkes feststeht, gehört [...] weiterführend erörtert und thematisiert.
Susanne Westenfelder, »Der Ursatz im Nebensatz«, in: kontrovers (21. April 2022),
abgerufen am 30. Januar 2025 (doi)
Quintenturm
Quintenturm und Scalar Shift
Beliebte Vorstellungen, um Tonarten interpretieren zu können, liegen in der Annahme einer räumlichen Vorstellung mit zwei verschiedenen Polen. Denn liegen Tonarten an auseinanderliegenden Polen wie z.B. hoch oder tief, lassen sich Begriffe über Bedeutungsnetze verknüpfen, die außermusikalische Interpretationen ermöglichen. Norbert Jürgen (heute: Enjott) Schneider hat dazu in seinem Aufsatz »Zeichenprozesse im Quintenzirkelsystem. Ein programmatischer Entwurf zur Semiotik der harmonisch-tonalen Musik« geschrieben (1979, S. 127):
Quintschritte von C abwärts werden als zum ›Dunklen‹, von C aufwärts als zum ›Hellen‹ führend empfunden, − hierin decken sich im Zeitraum von 1600 bis etwa 1900 die Aussagen von Komponisten sowie ästhetische Darstellungen (z. B. bei D. Schubart, E. T. A. Hoffmann) mit Aussagen der Musikpsychologie. Die damit implizierte semantische Entsprechung von ›unten‹ mit ›dunkel‹/›negativ‹ bzw. ›oben‹ mit ›hell‹/›positiv‹ gilt in der Psychologie für den abendländischen Raum als gesichert; die Konnotationsfelder ›Fallen‹, ›Sturz‹, ›Tod‹, ›Schwärze‹ für ›negativ‹ bzw. ›Sonne‹, ›Aufstieg‹, ›Licht‹ für ›positiv‹ sind nahezu interkulturell geläufig.
Folgende Harmoniefolgen wären Ausdruck für eine Bewegung in die Tiefe und könnten entsprechende außermusikalische Bedeutungen symbolisieren:
Während die in der nächsten Abbildung gezeigten Harmoniefolgen sich als Bewegung in die Höhe interpretieren lassen und entsprechende Interpretationen nahelegen :
David Temperley beobachtet Musik aus der Perspektive der Kognitionsiwssenschaften und versucht Preference-Rules für die Wahrnehmung von Musik zu bestimmen. Zum Beispiel lautet die erste well formed definition zur harmonischen Struktur eines Stückes: »A well-formed harmonic structure is a complete segmentation of a piece into non-overlapping chord-spans«. Annahmen dieser Art identifizieren die Funktion von Elementen mit ihrem musikalischen Material und da sich musikalische Parameter mit der Computer erforschen lassen, ist Temperleys Forschungsansatz als »computational modeling of music cognition« bekannt geworden. In seinem Aufsatz »Scalar Shift in Popular Music« beschreibt Temperley einen sogenannten scalar shift:
The idea is simple: The scale-degree content of a song (or a section of a song) tends to occupy a certain region on the “line of fifths,” the circle of fifths stretched out infinitely in both directions. Moving outside this region—especially if the move is emphasized (by rhythmic, textural, or other means) and involves multiple pitch classes—creates a sense of scalar shift. Such shifts may be momentary, as in the case of “Then Came You”; in other cases, they may be longer in duration, and may play a role in defining the large-scale formal structure of the song. I will argue, also, that scalar shifts often have interesting expressive implications—sometimes simply indicating a change in mood or situation, and sometimes carrying more specific emotional connotations, analogous to the expressive meanings of major and minor in common-practice music.
David Temperley, »Scalar Shift in Popular Music«, in: MTO 4/2011.
Die folgende Abbildung zeigt die Line-of-fifths representation in dem Song »A Hard Day's Night« von The Beatles (Lennon/McCartney):
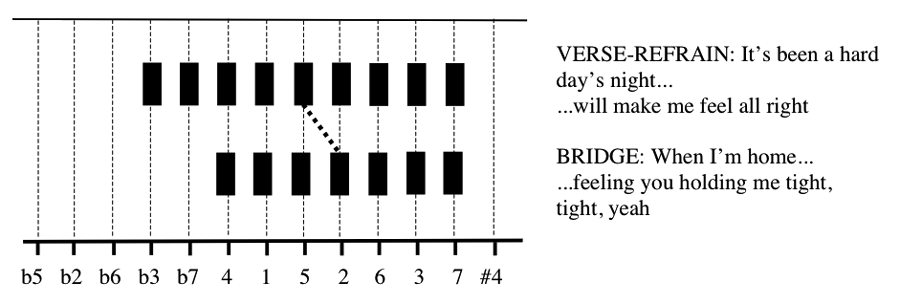
Abbildung aus: David Temperley, »Scalar Shift in Popular Music«, in: MTO 4/2011.
Wie Schneider interpretiert auch Temperley die Position in einer Quintenreihe symbolisch:
»given a constant tonic, a collection further in the ›sharp‹ direction on the line […] is generally perceived to be more happy. For present purposes, what is important is that the modes commonly employed in rock (Ionian through Aeolian) reflect a clear and gradual progression corresponding to their line-of-fifths order, with Ionian being happiest and Aeolian beeing saddest
Probleme
Unbestritten lässt sich Tonarten eine Semantik zuschreiben, die sich mit skalaren Modellen wie dem Quintenturm sowie damit einhergehenden Konnotationen trefflich veranschaulichen lässt. Das Problem dabei liegt in der Generalisierung bzw. in dem Verfahren, den Tonarten anhand des Quintenturms eine physikalisch-ontologische Eigenschaft zuzusprechen (z.B. E-Dur ist hell und c-Moll ist dunkel), obgleich diese Eigenschaften mit anderen Eigenschaften wie z.B. einer abwärtsführenden Bewegung oder einer tiefen Instrumentation konkurrieren können. Ohne Berücksichtigung des Kontextes wirken weitgehende Interpretationen einer physikalisch verstandenen Tonartencharakteristik beliebig.
Analysebeispiele zu diesem Thema kannst du in den folgenden Tutorials kennenlernen:
sinfonische Welle
Die ›sinfonische Welle‹
Richard Wagner nannte die Symmetrie vieler Musikstücke der zweiten Hälfte des 18. Jahrhunderts einmal abfällig Quadratur einer konventionellen Tonsatzkonstruktion. Versuche, die Musik Wagners und Bruckners mit neuen Modellen zu beschreiben, gehen in erster Linie auf August Halm (1869–1929) und Ernst Kurth (1886–1946) zurück. Die mit dem deutschen Musikpädagogen und österreichischen Musikwissenschaftler verbundene musikanalytische Richtung wird auch als musikalische Energetik oder musikalischer Energetismus bezeichnet. Damit ist gemeint, dass musikalische Form sich nicht mehr architektonisch, also in klar abgegrenzten Formteilen vermittelt, sondern nur im Auf- und Abbau von Spannung erlebt werden kann. In diesem Zusammenhang findet sich auch oft der Begriff Formung statt Form sowie die Metapher einer Welle: Denn eine idealtypische Welle bäumt sich auf (Spannungsaufbau), hat eine Krone (Spannungshöhepunkt) und verläuft sich wieder (Spannungsabbau). Die folgende Abbildung zeigt bei Ziehen des Sliders, dass sich der Kopfsatz der 1. Sinfonie in c-Moll Op. 11 von Felix Mendelssohn recht gut mithilfe einer Welle beschreiben lässt:
Felix Mendelssohn Bartholdy, Sinfonie Nr. 1 c-Moll op. 11, 1. Satz: Allegro di molto, Hochschulsymphonieorchester (München), Ltg. Marcus Bosch
Konzertmitschnitt mit Postproduktion der Hochschule für Musik und Theater München 2023, Lizenz: CC BY-SA 4.0
Warum sich die energetische Beschreibung von Musik als Methode der musikalischen Analyse nicht durchsetzen konnte, ist schwer zu sagen. Ein möglicher Grund für die unterbrochene Rezeption in der Nazizeit wurde oben im Zusammenhang mit der Funktionstheorie bereits angedeutet. Denn die Funktionstheorie wurde durch Musiktheoretiker mit brauner Vergangenheit wie Paul Schenk, Hermann Grabner und Wilhelm Maler breit rezipiert, während die Rezeption der energetischen Musiktheorie nach Kurth im Nazideutschland unterdrückt worden ist.
Seit den letzten Jahrzehnten des 20. Jahrhunderts gibt es eine Renaissance der in Deutschland verdrängten musikanalytischen Ansätze. Wolfgang Krebs hat sich dabei insbesondere um eine Weiterentwicklung des Instrumentariums einer energetischen Musikanalyse bemüht. An der eingangs abgebildeten Welle könnte kritisiert werden, dass sie zwar die Abfolge von lauten (spannungsreichen) und leisen (entspannteren) Teilen gut beschreibt, aber an den Kanten die energetische Wirkung nur sehr ungenau skizziert. Dem Auf und Ab der Welle lässt sich beispielsweise nicht entnehmen, ob ein lautes Ereignis kontinuierlich oder plötzlich eintritt usw. Im Folgenden siehst du vier Wellenformen. Für die ersten drei übernehmen wir die von Wolfgang Krebs vorgeschlagene Terminologie.
Die Fluktuationswelle
Das Kurvenbild einer Fluktuationswelle ist durch einen langsamen und fließenden Anstieg, einen Höhepunkt und eine wiederum langsame Rückentwicklung charakterisiert. Die Fluktuationswelle ist eine symmetrische Erscheinung mit einer Ausdehnung von 10, 20 oder mehr Takten. Ein solcher Spannungsverlauf findet sich beispielsweise im Kopfsatz der 6. Sinfonie Op. 68 (Pastorale)von Ludwig v. Beethoven:
Fluktuationswelle, Lizenz: CC0-1.0
Quelle: YouTube
Die Expansionswelle
Demgegenüber weist die Expansionswelle einen langsamen und kontinuierlichen Anstieg bis zu einem Höhepunkt auf. Der Wellenkrone folgt eine relativ schnelle Rückentwicklung. Die Expansionswelle ist daher asymmetrisch, ein schönes Beispiel für diesen Spannungsverlauf findet sich zum Beginn der 2. Sinfonie (Auferstehung) von Gustav Mahler:

Expansionswelle, Lizenz: CC0-1.0
Quelle: YouTube
Die Degressionswelle
Die Degressionswelle ist durch ein plötzliches Aufbäumen bzw. eine unvermitteltes Erscheinen (z.B. durch ein plötzlich einsetzendes Orchestertutti) charakterisiert. Auch sie ist asymmetrisch, jedoch mit einem Höhepunkt am Anfang, während ihr weiterer Verlauf eine ausführliche und relativ langsame Rückentwicklung zeigt. Degressionswellen sind in der Musik des ausgehenden 19. Jahrhunderts ausgesprochen häufig anzutreffen, ein solcher Spannungsverlauf findet sich beispielsweise in der 6. Sinfonie Op. 74 von Peter I. Tschaikowsky:

Degressionswelle, Lizenz: CC0-1.0
Quelle: YouTube
Die Blockwelle
Im Zusammenhang mit Instrumentalmusik des frühen 18. Jahrhunderts wird häufig von Terrassendynamik gesprochen. Dieser Begriff bezieht sich auf die Dynamik (also einen guten Indikator für eine hohe Spannung) und besagt, dass Lautstärkeverläufe nicht fluktuierend, sondern nach dem Modell einer Terrasse beschreibbar sind. Das Plateau der Terrasse entspricht dabei dem Parameter laut, die Umgebung dem Parameter leise. Wie die Fluktuationswelle sind Blockwellen symmetrische Erscheinungen, die einen plötzlichen Spannungsanstieg (wie die Degressionswelle) haben, aber darüber hinaus auch einen schnellen Spannungsabbau (wie die Expansionswelle). Das folgende Beispiel zeigt einen Blockwellenverlauf in der Sinfonie Hob. I:100 (Militär) von Joseph Haydn:

Blockwelle, Lizenz: CC0-1.0
Quelle: YouTube
Die hier vorgestellten Wellenformen bilden ein gutes Instrumentarium zur Erschließung der Form höchst komplexer Orchestermusik (beispielsweise um 1900). Die Aufgabe einer wissenschaftlichen Beschäftigung mit Musik könnte es darüber hinaus sein, Modelle der Aufeinanderfolge von Wellen zu konstruieren, um so Zeit- und Personalstile theoretisch zu erschließen und deren Wirkung besser verstehen zu können. Und nicht zuletzt bieten die gezeigten Wellenformen ein methodisches Werkzeug, um im Musikunterricht allgemeinbildender Schulen Orchestermusik zu thematisieren, deren Komplexität und Länge einer Notenanalyse entgegensteht. Nicht zuletzt lassen Spannungsverläufe eine Harmonisierung von emotionalem Erleben und theoretischem Beschreiben zu, was sich durch kein anderes musiktheoretisches Werkzeug in vergleichbarem Maße bewerkstelligen lässt. Die Konzentration auf den Spannungsverlauf einer musikalischen Passage ist zudem hilfreich, größere musikalische Abschnitte als Einheiten aufzufassen, wie das abschließende Beispiel aus dem Vorspiel zum 1. Akt der Oper Tristan und Isolde von Richard Wagner zeigt:
Tristan und Isolde | Wellenform des Vorspiels, Lizenz: CC0-1.0
Quelle: YouTube
Forensische Analyse
Die Forensische Analyse
Helmut Rösing schrieb über die Forensische Analyse
Forensische Popmusik-Analyse ist immer vergleichend. Ausgangspunkt sind zwei Musikstücke: ein urheberrechtlich geschütztes Original und ein später entstandenes Stück, in dem angeblich urheberrechtlich geschütztes Material Verwendung gefunden hat. Was der Kläger diesbezüglich vorbringt, versucht die Seite der Beklagten zu widerlegen.
Die Argumentation des Klägers vollzieht sich in der Regel in zwei Schritten, um eine Urheberrechtsverletzung so plausibel wie möglich nachzuweisen. Erstens muss deutlich gemacht werden, dass das Originalwerk eine eigenschöpferische Qualität und Wertigkeit besitzt. Grundlage dafür ist die minutiöse Analyse kleinster Musikpartikel, die aus kunstmusikalischer Sicht als eher trivial oder banal abgetan zu werden pflegen, hier aber als Indikatoren für musikalische Prägnanz stehen: Aus musikstrukturellen ›Kleinigkeiten‹ kann eine Motivsemantik erwachsen, die für geistiges Eigentum kennzeichnend ist [...]
Die Abwehrstrategie der Beklagtenseite besteht darin, diese Eigentümlichkeiten klein zu reden. Als Beleg wird gerne auf die Nähe zu volkstümlichem und damit urheberrechtsfreiem Liedgut verwiesen. Oder aber auf angeblich vergleichbare Partien aus so genannten klassischen Kompositionen. Im Vergleich mit deren Strukturen wird dann die Machart des Poptitels als banale Anwendung rein handwerklicher Musikbetätigung abgetan.
Helmut Rösing, »Forensische Popmusik-Analyse«, in: Black Box Pop, Bielefeld 2012, S. 257-258.
Selbst dann, wenn man Helmut Rösing in seiner Diagnose über das Wesen der Pop-Rockmusik nicht folgen mag, weil diese einem veralteten Musiktheorie-Verständnis verpflichtet ist und die eigene Beobachter-Position nicht angemessen reflektiert, sind seine Erläuterungen zur Forensischen Popmusik-Analyse präzise und getragen von reichen Erfahrungen in diesem Bereich. Als Methoden verwendet Rösing in seinem Aufsatz vergleichende Transkriptionen (und bedient sich damit sehr konventionellen Methoden der musikalischen Analyse) sowie technische Verfahren zur Soundanalyse (unter Zuhilfenahme einschlägiger Audio-Software).


