Intonation und historische Stimmungen

Wenn es um Intonation geht, geht es zunächst grob gesagt um feine Tonhöhenunterschiede. Diese feinen Unterschiede lassen sich bestimmen und in der Einheit Cent angeben. Alexander John Ellis hat diese Einheit 1875 zum ersten Mal verwendet und folgendermaßen definiert: 1 Cent ist der hundertste Teil eines Halbtonschrittes der gleichstufig temperierten Stimmung (also der heute üblichen Stimmung des Klaviers).

Wer die Wahrnehmung feiner Tonhöhenunterschiede trainieren will, kann dies hier tun. Feine Tonhöhenunterschiede können sich in der Musik sehr unterschiedlich auswirken, je nachdem in welchem Zusammenhang sie vorkommen. Davon handelt das folgende Tutorial.

Der griechische Philosoph Pythagoras (6. Jh. v. Chr.) ist heute vor allem als Mathematiker bekannt, beschäftigte sich jedoch − zumindest der Überlieferung nach − auch mit Musiktheorie. Auf ihn beruft man sich, wenn man von der ›pythagoräischen Quinte‹ (oder auch ›pythagoreischen Quinte‹) spricht:

Die Pythagoräische Quinte wird auch reine Quinte genannt. Die beiden Töne, Quintton und Grundton, haben Frequenzen, deren Werte im Verhältnis 3 : 2 stehen. Bei einer reinen Quinte verschmelzen die beiden Töne so sehr, dass man das Quintintervall fast als Einheit wahrnimmt. Diese Quinte kommt in der Obertonreihe vor, sie ist gewissermaßen naturgegeben.

Auch wenn man zwischen diesen beiden Arten von Quinten zunächst kaum einen Unterschied hören kann: Reine Quinten wären für den Quintenzirkel zu groß! Das kann man sich am besten am Quintenturm klarmachen: Wenn man von einem beliebigen Ton ausgeht − in unserem Beispiel ist es der Ton es − und 12 Quinten aufeinander türmt, erreicht man einen Zielton − in unserem Beispiel dis. Die Töne dis und es liegen auf dem Klavier auf der selben Taste, sie sind, enharmonisch betrachtet, der gleiche Ton (enharmonische Verwechslung). So könnte man zunächst annehmen, 12 Quinten seien ganz einfach dasselbe wie 7 Oktaven.

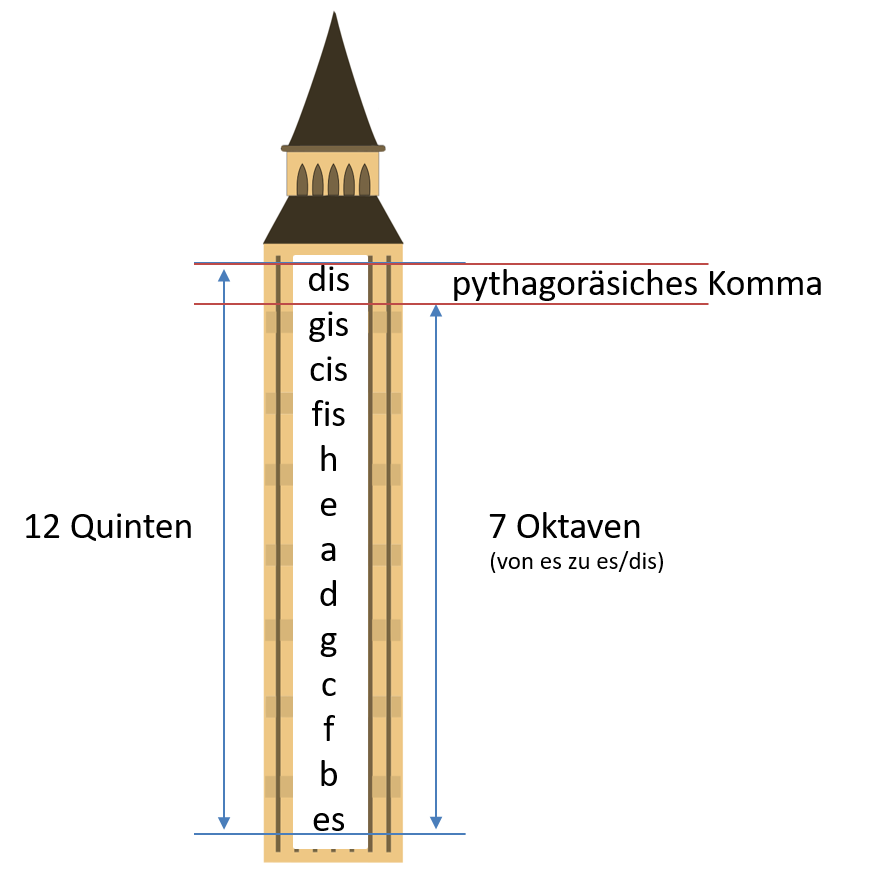
Wenn man allerdings reine Quinten verwendet, stimmt diese Rechnung nicht. Mit reinen Quinten erreicht man einen Zielton, der merklich höher ist als die Oktavierung des Ausgangstones. 12 reine Quinten schießen sozusagen über das Ziel hinaus, der Quintenturm ist in diesem Fall um etwa 23,5 Cent (das berühmte Pythagoräische Komma) höher als 7 Oktaven. Oder anders formuliert: Reine Quinten ergeben keinen Quintenzirkel, sie sind dafür zu groß. Der Kreis schließt sich nicht.

Wenn der Kreis sich aber schließen soll, dann kann man die einzelnen Quinten unmerklich verengen und erreicht nach 12 Quinten genau die Oktavierung des Ausgangstones. Man verteilt also das pythagoräische Komma gleichmäßig auf die zwölf Quinten. Diese Verengung beträgt ziemlich genau zwei Cent und ist bei der einzelnen Quinte kaum wahrnehmbar, jedenfalls wird sie von den Wenigsten als störend empfunden.

Wir haben damit die Grundlagen zweier wichtiger Stimmungssysteme kennengelernt:

• der pythagoräischen Stimmung (mit reinen Quinten, bei denen sich der Quintenzirkel nicht schließt)
• und der gleichstufig temperierten Stimmung (mit gleichmäßig um ca. 2 Cent verengten Quinten, bei der sich der Quintenzirkel schließt).

Historisch betrachtet ist die pythagoräische Stimmung das Stimmungssystem des Mittelalters, die gleichstufig temperierte Stimmung ist seit fast 200 Jahre das Stimmungssystem der Gegenwart. Diese und ähnliche Systeme sind aber keinesfalls nur historisch gesehen von Interesse. Sie sind ganz allgemein ›Intonationsideen‹, die sich je nach musikalischem Kontext mehr oder weniger eignen. Sehr anschaulich werden solche intonatorischen Systeme, wenn man sie sich nicht als Zirkel oder Turm vorstellt, sondern auf einer Klaviertastatur.

Diese und ähnliche Arten der Darstellung mit Hilfe von Klaviertastaturen spielen auch bei moderner Musiksoftware eine Rolle, z. B. im microtuning tool einer DAW (Digital Audio Workstation wie z.B. Cubase, Logic, Ableton Live u.a.). Nun ist es wichtig zu wissen, dass solche Darstellungen nicht von reinen Quinten ausgehen, wie es vielleicht historisch zunächst überzeugender wäre, sondern von den temperierten Quinten der gleichstufigen Temperatur. Diese gilt als Normalfall und Ausgangspunkt. Alle Abweichungen von der Gleichstufigkeit werden in Cent angegeben und auf die jeweilige Taste der Klaviertastatur geschrieben:

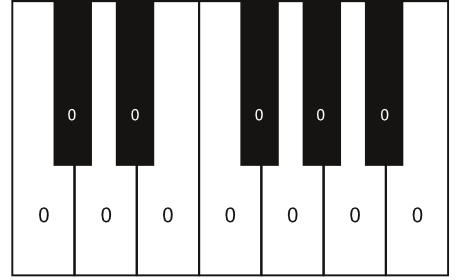
Steht auf jeder Taste der Wert 0, so handelt es sich um eine gleichstufig temperiert gestimmte Tastatur. Will man dagegen die pythagoräische Stimmung darstellen, sieht die Graphik so aus (vom Kammerton a aus gerechnet):

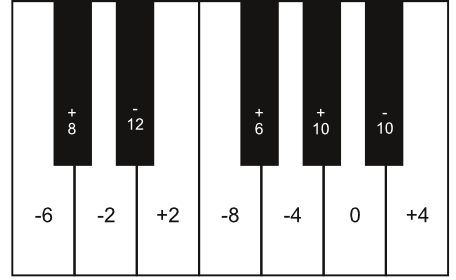
Alle Quinten bis auf eine sind in dieser Stimmung reine Quinten. Am besten erkennt man dies, wenn man von a aus im Quintenturm nach oben denkt: Auf der Taste e steht der Wert 2, e ist also als reine Quint über a gestimmt. Der Quintton über e heißt h. Er benötigt dann bereits den Wert 4, um zum Ton e eine reine Quint zu bilden, etc. Die Quint unter a heißt d. Da a nicht verändert werden soll, benötigt man ein d, das um zwei Cent tiefer ist als der gleichstufig temperierte Wert, etc. An einer Stelle sieht man, das sich der Kreis nicht schließt: Zwischen gis (+10) und es (-12). Dieses Intervall klingt unangenehm verstimmt, wird nicht verwendet und wird als ›Wolfsquinte‹ bezeichnet. Je nachdem, von welchem Startton man ausgeht, könnte die ›Wolfsquint‹ auch an einer anderen Stelle des Systems zu liegen kommen. Sie ist gewissermaßen der Preis, den man für die Reinheit der übrigen Quinten zahlt.

Wenn man nun die pythagoräische Stimmung näher untersucht, bemerkt man außer den reinen Quinten und der einen Wolfsquint weitere Besonderheiten. Innerhalb der C-Dur-Tonleiter sieht und hört man deutlich:

• Die Leittonschritte (e-f und h-c) sind sehr eng. Die Ganztonschritte (c-d, d-e, f-g, g-a, a-h) sind sehr weit. Meist wird dies als melodisch angenehm und als saubere Intonation empfunden. Die pythagoräische Stimmung gilt als besonders geeignet für Melodien.
• Die großen Terzen (c-e, f-a, g-h) sind ziemlich weit. Erklingen die beiden Töne einer großen Terz gleichzeitig, zum Beispiel innerhalb eines Dreiklangs, wird die Intonation meist als gerade noch erträglich eingestuft. Die pythagoräische Stimmung gilt als nicht besonders geeignet für Harmonien.

Die pythagoräische Stimmung, so könnte man grob zusammenfassen, eignet sich also für Melodien, aber nicht für Harmonien. Dass sie sich für Harmonien so wenig eignet, liegt an den großen Terzen. Diese sind zu weit, um rein zu klingen. Will man nun auf reine Großterzen nicht verzichten, steht ein anderes Stimmungssystem zur Verfügung: die mitteltönige Stimmung.

Die mitteltönige Stimmung ist historisch betrachtet die Stimmung des 16. und 17. Jahrhunderts. Sie existiert in verschiedenen Varianten. Die wichtigste davon geht von der reinen Großterz aus. Die beiden Töne dieser Terz, Terzton und Grundton, haben Frequenzen, deren Werte im Verhältnis 5 : 4 stehen. Diese Terz kommt in der Obertonreihe vor, auch sie ist, wie die reine Quint, gewissermaßen naturgegeben.

Will man durch das Stapeln von Quinten im Quintenturm solche Großterzen erzielen, muss man jede Quinte verengen, und zwar noch stärker verengen als in der gleichstufig temperierten Stimmung. Schritt für Schritt von a aus gedacht:

• Die Großterz über a heißt cis.
• Im Quintenturm ist cis von a vier Schritte entfernt. (a-e, e-h, h-fis, fis-cis)
• Der Terzton soll eine reine Terz zum Grundton bilden, cis soll also um 14 Cent tiefer sein als in der gleichstufig temperierten Stimmung.
• 14 Cent verteilt auf 4 Quinten bedeuten 3,5 Cent Verengung für jede Quint.

Die mitteltönige Stimmung lässt sich auf der Klaviertastatur demnach darstellen wie folgt:

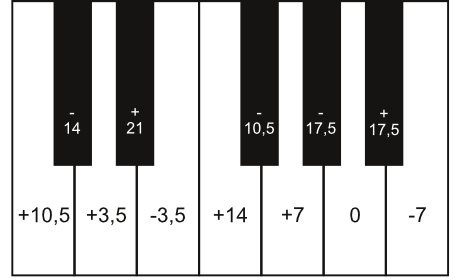
Alle Quinten bis auf eine sind in dieser Stimmung um 3,5 Cent enger als Quinten in der gleichstufig temperierten Stimmung. Dadurch wird ein Ziel erreicht: Die meisten großen Terzen, genau 8 von 12 möglichen, sind rein. Man kann es an den Werten der Tastatur ablesen, es sind die Terzen über es, b, f, c, g, d, a und e.
An einer Stelle sieht man, dass sich auch in der Mitteltönigkeit der Kreis des Quintenzirkels nicht schließt: Zwischen gis (-17,5) und es (+21). Auch dieses Intervall wird als ›Wolfsquinte‹ bezeichnet. Je nachdem von welchem Startton man ausgeht, könnte auch die ›Wolfsquint‹ der mitteltönigen Stimmung an einer anderen Stelle des Systems zu liegen kommen. Außerdem sind einige Großterzen nicht spielbar: h-es, fis-b, cis-f und gis-c werden als ›Wolfsterzen‹ bezeichnet und sind viel zu weit, als dass das Ohr sie toleriert.
Wenn man nun die mitteltönige Stimmung noch näher untersucht, bemerkt man außer den verengten Quinten, den reinen Großterzen, der ›Wolfsquint‹ und den ›Wolfsterzen‹ weitere Besonderheiten. Innerhalb der C-Dur-Tonleiter sieht und hört man deutlich:

• Die Leittonschritte (e-f und h-c) sind sehr weit. Die Ganztonschritte (c-d, d-e, f-g, g-a, a-h) sind ziemlich eng. Meist wird dies als melodisch nicht besonders sauber intoniert empfunden. Die mitteltönige Stimmung gilt also als nicht besonders geeignet für Melodien.
• Die großen Terzen (c-e, f-a, g-h) sind ziemlich eng, das heißt rein. Erklingen die beiden Töne einer großen Terz gleichzeitig, zum Beispiel innerhalb eines Dreiklangs, ist der Verschmelzungsgrad hoch. Die mitteltönige Stimmung gilt als besonders geeignet für Harmonien.

Aufgaben zum Intonationshören